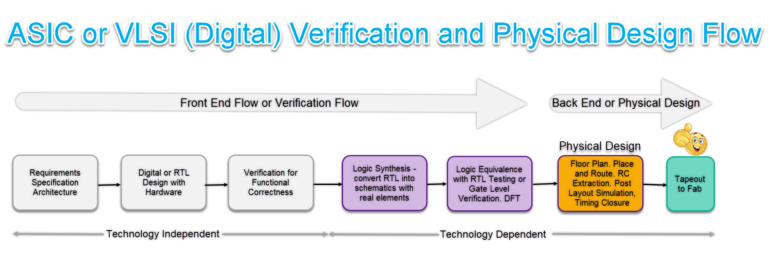
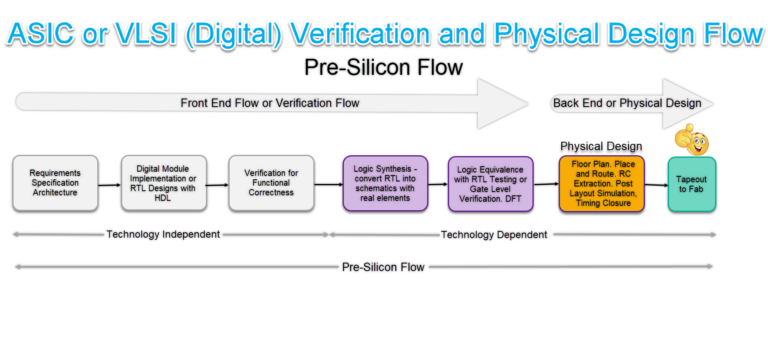
Physical Design Flow
Device Basics – Passive Elements/Devices
In this section we are going to read some basics of electrical engineering and semiconductor physics before jump into Physical Design or layout of the IC design.
First thing you need to know is Physical Design is not a rocket science. Anyone who have basic knowledge of electrical/electronics engineering can learn easily with little effort. Remove the fear of failure in your mind and start learning with excitement and will reward you once you learn and practice with the free tools available on the internet. We will list out all the free or open source tools available at the end of this article or at the each stage of the design cycle.
There are 2 main components we need to focus in Physical Design
- Resistor
- Capacitor
Resistor
Resistor is a passive 2 terminal electronic component/device which opposes the flow of electrons or electrical current. Resistance is measured in Ohms.
Symbol of a Resistor:
According to ohm’s law to find out the resistance is:
R = V/I where R = Resistor V = Voltage I = Current
Resistivity:
It is the measure of the ability of a material to oppose the flow of current.
Formula to find Resistivity of conductors for uniform cross section is:
ρ = RA/I where ρ = Resistivity R = Resistance a = cross sectional area of the conductor l = length of the conductor
Capacitor
A capacitor is a passive 2 terminal electronic component which stores energy in the form of electrostatic energy. It is measured in Farads it consists of 2 conducting plates separated by a dielectric (insulating material).
Symbol of Capacitor:
Formula to find capacitance is:
C = εr ε0 A/d where c = capacitance ε0 = permittivity of free space εr = permittivity of dielectric medium d = distance between the plates A = area of the 2 conducting plates.
Types of capacitances:
- Area Capacitance
- Fringing Capacitance
- Coupling Capacitance
Note: Capacitor plays a major role in physical design of semiconductor devices.
Area Capacitance
Area capacitance is formed among the metal interconnects and base layer. Here, base layer acts as a one conducting plate and metal layer acts as 2nd conducting plate and in between the area is filled by dielectric material. So, there forms some capacitance which is consider as area capacitance. Based on the above statement, we can say the bottom metal interconnect layer carries more capacitance compared to top metal interconnect layers. Because we know that gap between the conducting plates leads to less capacitance.
If you see the below example, Metal 2 is near (d=distance is less) to base layer compared to Metal 4 ( d=distance is more). So, Metal 2 will have more area capacitance compared to Metal 4 as per the formula C = εr ε0 A/d , where d = distance between between the base layer to metal layer.
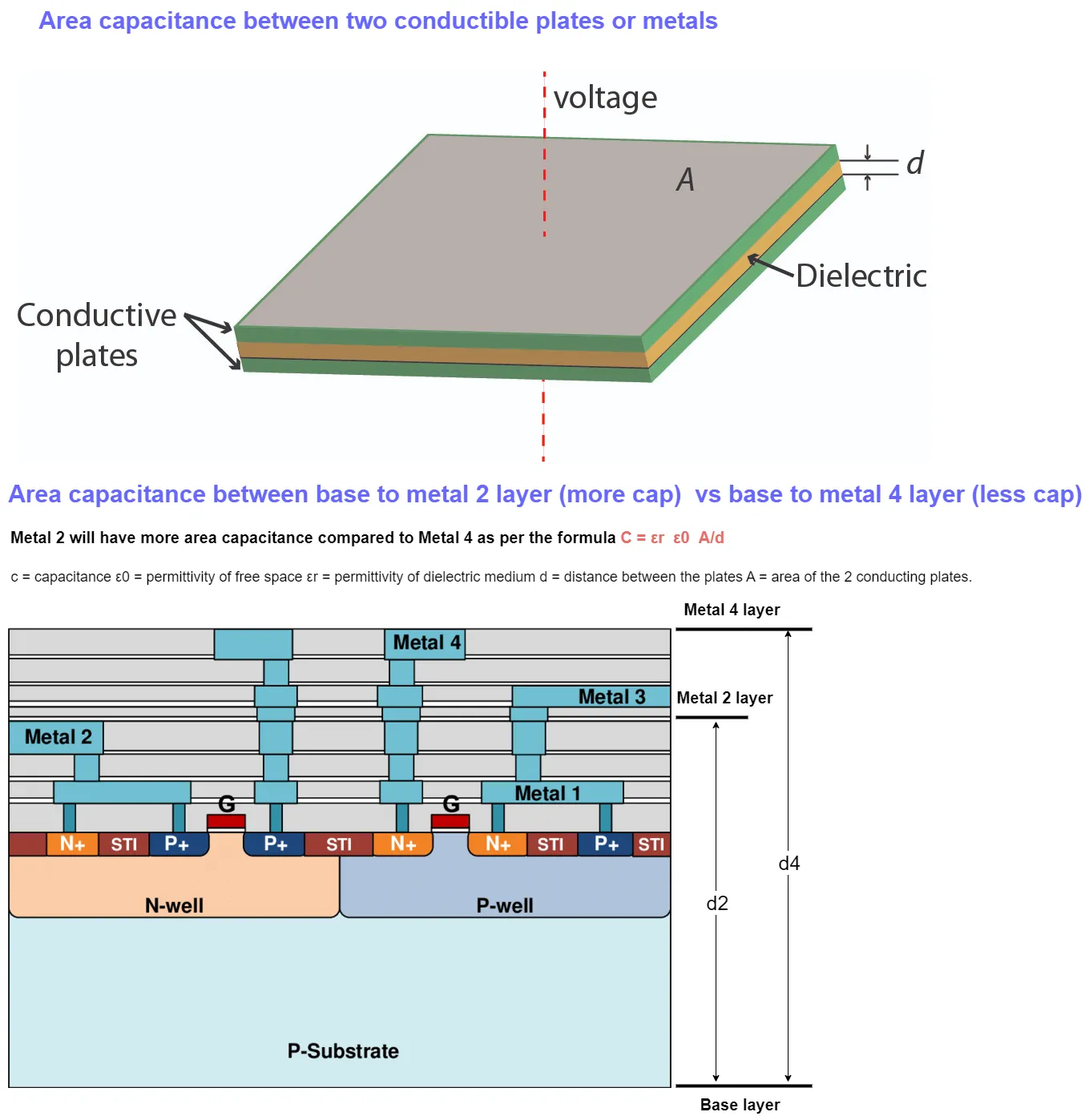
Formula of Area capacitance:
C Area= (∈ L W)/h where ∈ = permittivity L = Length of the wire W = Width of the wire h = height
Fringing Capacitance
Fringing capacitance another name is side wall capacitance. It is also similar to area capacitance but only difference is the capacitance can be considered from base to sides of the metal layers. You can see the following image for better understanding.
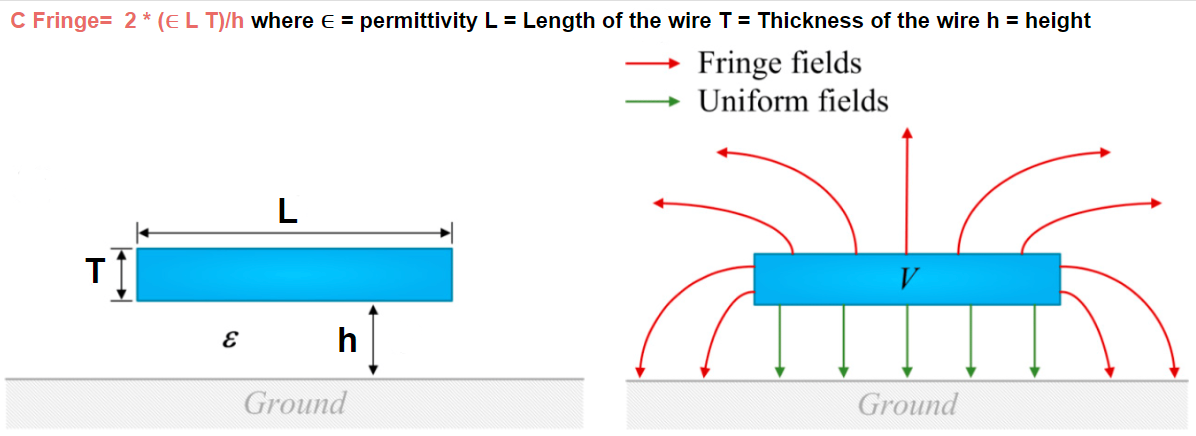
Formula for Fringing capacitance:
C Fringe= 2 * (∈ L T)/h where ∈ = permittivity L = Length of the wire T = Thickness of the wire h = height
Coupling Capacitance
Coupling capacitance is formed in between the nets in the same layer. If 2 nets are running parallel for long distance in the same metal layer then coupling capacitance will be formed. Coupling capacitance should be less as much as possible because it is reason for the crosstalk in the design.
Following image shows an example for the coupling capacitance.
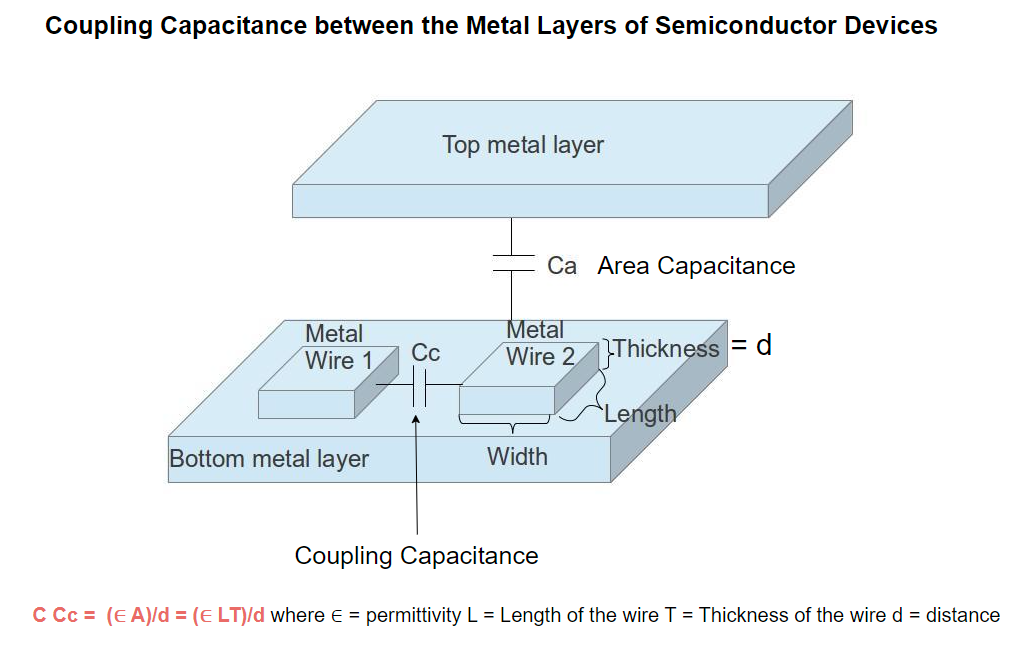
Formula for Coupling capacitance:
C Cc= (∈ A)/d = (∈ LT)/d where ∈ = permittivity L = Length of the wire T = Thickness of the wire d = distance
Propagation Delay
Propagation Delay or the Wire Delay or The Net Delay is nothing but the time takes for the input signal to reach its output The reason for this delay is due to internal resistance and capacitances For example if we turn on the light it won’t glow immediately it takes some time the input we given to reach its output but generally we didn’t notice that delay the delay is very very less Lets see more detail how the delay happens.
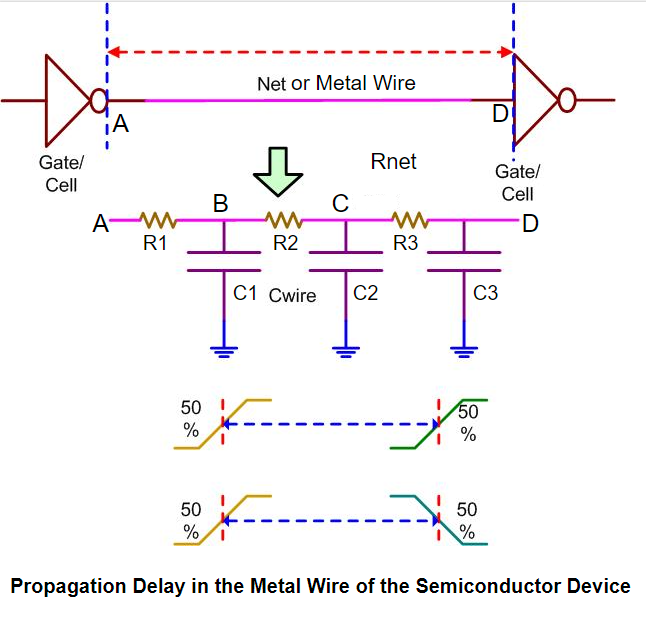
The above circuit represents a conductor (wire) which consists of internal capacitances and resistance. Let us assume it as a wire, point A is the starting point where we give input similarly, point D is the ending point where we take output. If we applied input it goes through R1 and C1 before going to R2 it takes some time to charge at C1 and the process goes on until the given input is reaches to output (point D) Here we have to focus on two things mainly first one is the length of the wire increases the number of internal resistances and capacitances increases it takes more time to reach output because of capacitors charging and discharging. The second thing is because of more resistances the input which we have given might not be exact when it reaches to output due to loss in travelling. So here we got to know that issues what we faced while using long wires the solution for this is adding buffers in between the long wires. Here the buffer acts as repeater and used to reproduce the input signal.
Elmore Delay
Elmore proposed an approximate way of calculating the delay of a network consists of resistors & capacitors (Distributed Networks) Following this we can find out the delay of a wire by dividing the wire into smaller segments without loosing much of accuracy for a length of wire L, if r and c are the resistance per unit length and capacitance per unit length, the Elmore delay of the wire = (rcL)2 (rcL to the power of 2)
Here is the example for Elmore delay have a look.
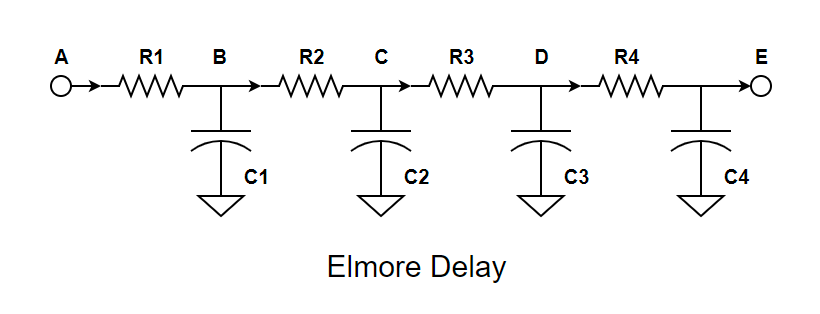
The delays:
From A to B: R1(C1+C2+C3+C4)
From A to C R1(C1+C2+C3+C4) + R2(C2+C3+C4)
From A to D R1(C1+C2+C3+C4) + R2(C2+C3+C4) + R3(C3+C4)
From A to E R1(C1+C2+C3+C4) + R2(C2+C3+C4) + R3(C3+C4) +R4C4
From B to C R2(C2+C3+C4) From C to E R3(C3+C4) + R4C4
By using this Elmore delay we are going to find delays in the upcoming examples. In the next part of basics we will see about MOSFET.